WEB TUTORIAL - Group Theory

H₂O Worked Example

Applying the Reduction Formula

C2v	E	C2 (z)	v(xz)	v(yz)	Linear functions, rotations	Quadratic functions	Cubic functions
A1	+1	+1	+1	+1	z	x2, y2, z2	z3, x2z, y2z
A2	+1	+1	-1	-1	Rz	xy	xyz
B1	+1	-1	+1	-1	x, Ry	xz	xz2, x3, xy2
B2	+1	-1	-1	+1	y, Rx	yz	yz2, y3, x2y

Number of symmetry elements, h = 4

Now we have all of the required parts, we simply put them together into the Reduction Formula one row at a time.

It is worth doing this on a piece of paper rather than in your head before checking your answers!

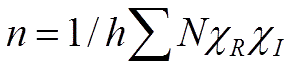
Key: The numbers in each representation are: N x _R x _I

To calculate the number of A₁ representations we focus on the values of _I for this representation, which are +1 for each operation.
For E: 1 x 2 x 1 = 2
For C₂: 1 x 0 x 1 = 0
For _v(xz): 1 x 2 x 1 = 2
For _v'(yz): 1 x 0 x 1 = 0
The summation of these terms is 4 (2+0+2+0). The number of symmetry elements (h Term) is 4, and hence the number of A₁ representations is: 1/h x (4) = 1.

To calculate the number of A₂ representations we focus on the values of _I for this representation, which are +1, +1, -1, -1.
For E: 1 x 2 x 1 = 2
For C₂: 1 x 0 x 1 = 0
For _v(xz): 1 x 2 x -1 = -2
For _v'(yz): 1 x 0 x -1 = 0
The summation of these terms is 0.

To calculate the number of B₁ representations we focus on the values of _I for this representation, which are +1, -1, +1, -1.
For E: 1 x 2 x 1 = 2
For C₂: 1 x 0 x -1 = 0
For _v(xz): 1 x 2 x 1 = 2
For _v'(yz): 1 x 0 x -1 = 0
The summation of these terms is 4 (2+0+2+0). The number of symmetry elements (h Term) is 4, and hence the number of B₁ representations is: 1/h x (4) = 1.

To calculate the number of B₂ representations we focus on the values of _I for this representation, which are +1, -1, -1, +1.
For E: 1 x 2 x 1 = 2
For C₂: 1 x 0 x -1 = 0
For _v(xz): 1 x 2 x -1 = -2
For _v'(yz): 1 x 0 x 1 = 0
The summation of these terms is 0.

So there is one A₁ and one B₁ representation.
So what does this mean? ⇒